GMDH Neural Network

Every once in a while, a technique comes along that takes the data science community by storm. The General Method of Data Handling (GMDH) type neural networks are an example of such a technique. It was developed behind the “Iron Curtain” during the days of Soviet Union. Back in the day it was not widely known or taught but today, it seems strange that such a powerful technique went almost unnoticed. - N.D. Lewis

Introduction

The GMDH Method models the relationship between a set of ‘p’ attributes and ‘y’ a target variable using a multi-layered perceptron-type neural network structure. So, with respect to time series, the algorithm learns the relationship among the lags.

In general, the connection between the input and output variables can be approximated by an infinite Volterra-Kolmogrov-Gabor polynomial form.

However, A.G. Ivakhnenko (The ‘Father of Deep Learning’ and developer of this technique) showed that a 2nd-order polynomial with a feedforward perceptron can be used to approximate this connection. The 2nd-order polynomial which looks like -

Here, \('Y'\) Response Variable, \(x_i\) and \(x_j\) are the lagged time series values.

Network Structure

In the GMDH type Neural Network, there are three components -

Input Layer,
Hidden Layers and
A Final Output Layer.

The Input Layer is where the network is fed with inputs i.e. the lagged time series values into the network. The GMDH algorithm considers all pairwise combinations of ‘p’ lagged values. Therefore, each combination \(^pC_2\) i.e. \(p(p-1)/2\) enters each neuron.

The Hidden Layer(s) contain nodes or neurons. Inside the neuron, a function \(f(x)\) takes the input performs the below calculation to give an output \(Y_ij\).

Here, the coefficients \(\alpha_{(s)}\) are weights. It is very crucial that we have optimal values of these weights. The algorithm uses the training set to estimate these coefficients, then, rank them by Mean Squared Error (MSE) and finally choose the best values.

In a GMDH network the 1st Hidden Layer consists of a set of Quadratic Functions of inputs, the 2nd Hidden Layer involves 4th Degree Polynomial, 3rd Hidden Layer involves 8th degree and so on. So, the network becomes progressively complex with every training example.

However, there is a problem! Practically, to account for so many neurons and computing such complex polynomials can be very time-consuming and not feasible. To overcome this, the end-user (Me and You) has to select the number of inputs amd layers to be included in the model. This role of end-user deciding what the network structure is going to look like is an example of Inductive Bias.

Inductive Bias is anything that causes an inductive learner (Me and You) to prefer some hypothesis over other hypothesis (here, one structure over another).

Note : GMDH networks are not fully inter-connected. Nodes with little predictive power are dropped !

Let’s build a GMDH type Neural Network for our U.S. Electricity Consumption Time Series.

Data Preparation

data = read.csv("data.csv")[,3]
date = read.csv("data.csv")[,1]
date = as.Date(date, format = "%d/%m/%Y")

train1 = ts(as.matrix(data[136:236]),end=c(2020,8), frequency = 12)
y1 = data[237:241] #to be predicted
train2 = ts(as.matrix(data[141:241]),end=c(2021,1), frequency = 12)
y2 = data[242:246] #to be predicted
train3 = ts(as.matrix(data[146:246]),end=c(2021,6), frequency = 12)
y3 = data[247:248] #to be predicted

require(GMDH); require(Metrics)

GMDH Network

Here we use GMDH package to train the neural network.

GMDH Neural Networks are meant for short-term prediction. In R, we can make at most 5 predictions only.

To ensure that we can compare GMDH network with others we train 3 networks for each model to predict 5 + 5 + 2 = 12 values.

1st, we use 100 values (136 to 236) from Apr,2012 to Aug,2020 and predict 5 values from (237 to 241) Sept,2020 to Jan,2021.
2nd, we use 100 values (141 to 241) from Sept,2012 to Jan,2021 and predict 5 values from (242 to 246) Feb,2021 to June,2021.
3rd, we use 100 values (146 to 246) from Feb,2013 to June,2021 and predict 2 values from (247 & 248) July -&- Sept,2021.

Each model has different input and layer inputs.

The 1st model has 22 inputs with 5 layers.
The 2nd model has 22 inputs with 4 layers.
The 3rd model has 08 inputs with 2 layers.

The models are fitted using the fcast function which has 4 core arguments:

1st : training and test sample used to build model
2nd : number of inputs into the network
3rd : number of layers
4th : number of predictions to make

### Model_1 (22,5)
set.seed(2018)
fit_1a = fcast(train1, input = 22, layer = 5, f.number = 5)# 237-241 values
fit_1b = fcast(train2, input = 22, layer = 5, f.number = 5)# 242-246 values
fit_1c = fcast(train3, input = 22, layer = 5, f.number = 2)# 247-248 Values
### Model_2 (22,4)
set.seed(2018)
fit_2a = fcast(train1, input = 22, layer = 4, f.number = 5)# 237-241 values
fit_2b = fcast(train2, input = 22, layer = 4, f.number = 5)# 242-246 values
fit_2c = fcast(train3, input = 22, layer = 4, f.number = 2)# 247-248 Values
### Model_3 (8,2)
set.seed(2018)
fit_3a = fcast(train1, input = 8, layer = 2, f.number = 5)# 237-241 values
fit_3b = fcast(train2, input = 8, layer = 2, f.number = 5)# 242-246 values
fit_3c = fcast(train3, input = 8, layer = 2, f.number = 2)# 247-248 Values

Extracting Results

Here we combine the predicted values along with respective 95% Confidence Intervals.

model.1 = c(as.numeric(fit_1a$mean), as.numeric(fit_1b$mean), as.numeric(fit_1c$mean))
upper.1 = c(fit_1a$upper,fit_1b$upper,fit_1c$upper)
lower.1 = c(fit_1a$lower,fit_1b$lower,fit_1c$lower)
#
model.2 = c(as.numeric(fit_2a$mean), as.numeric(fit_2b$mean), as.numeric(fit_2c$mean))
upper.2 = c(fit_2a$upper,fit_2b$upper,fit_2c$upper)
lower.2 = c(fit_2a$lower,fit_2b$lower,fit_2c$lower)
#
model.3 = c(as.numeric(fit_3a$mean), as.numeric(fit_3b$mean), as.numeric(fit_3c$mean))
upper.3 = c(fit_3a$upper,fit_3b$upper,fit_3c$upper)
lower.3 = c(fit_3a$lower,fit_3b$lower,fit_3c$lower)
#
test = tail(data,12) #Actual Values

Plot of All 3 Networks

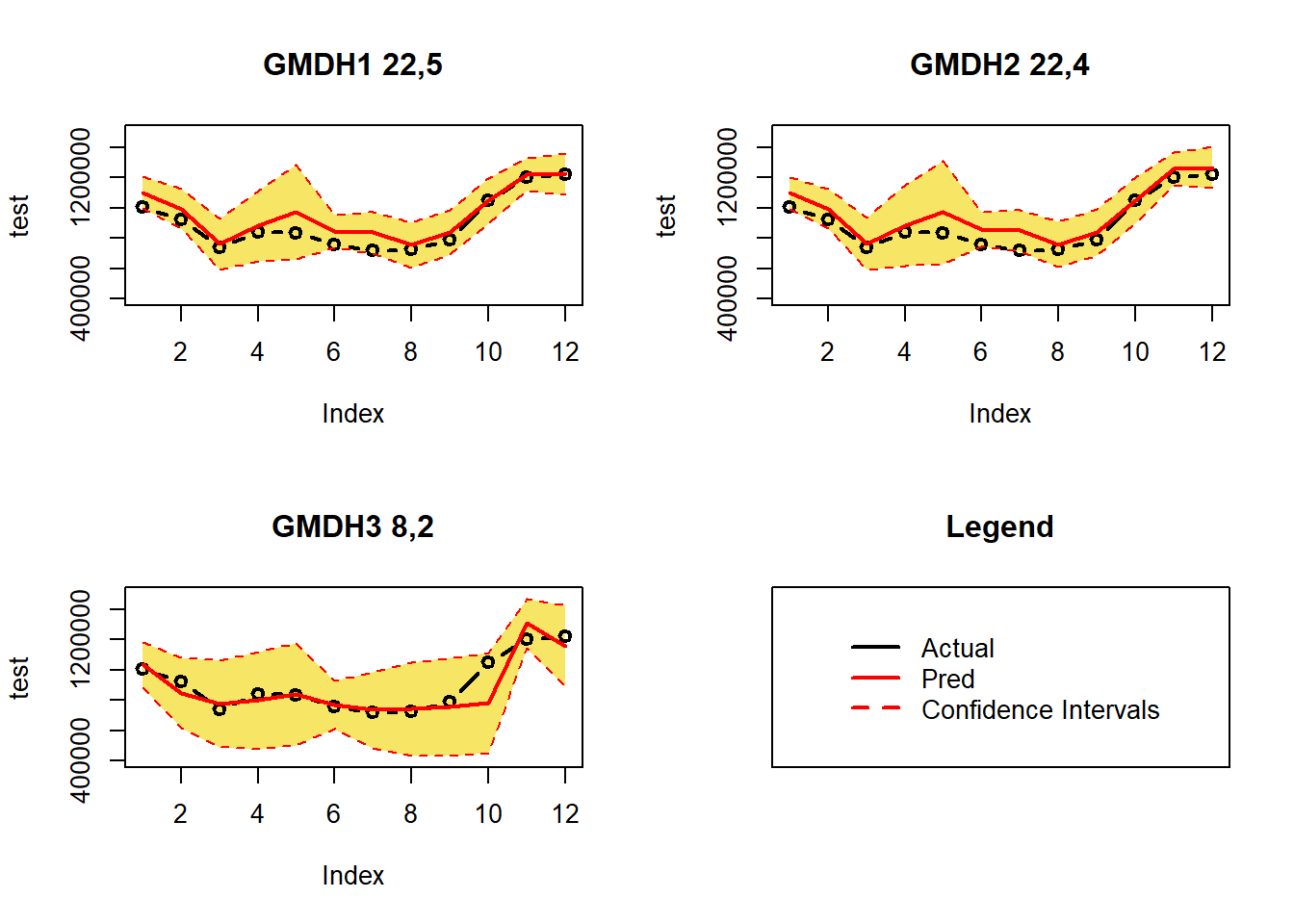
For all 3 plots, the Actual Values lie inside the 95% Confidence Intervals indicating that the models are good.

RMSE-MAPE

round(c(rmse(test, model.1) ,mape(test, model.1), 
        rmse(test, model.2) ,mape(test, model.2),
        rmse(test, model.3) ,mape(test, model.3)),5)

## [1] 71444.44743     0.06892 77453.65509     0.07800 91328.53246     0.06016

RMSE and MAPE values are pretty low. We select the models with the lowest RMSE and MAPE figures.

Based on MAPE, we would select the 3rd network with lowest MAPE of 6%
Based on RMSE, we would select the 1st network with lowest RMSE of 71,444.45

Final Output

U.S. Consumption of Electricity Generated by Natural Gas
Dates	Actual¹	GMDH.1¹	GMDH.2¹	GMDH.3¹
2020-09-01	1006071.1	1102578.3	1098753.5	1034773.8
2020-10-01	924056.2	993342.3	994504.3	848490.6
2020-11-01	737935.2	759993.1	762124.1	774978.5
2020-12-01	839912.6	880570.2	883286.8	798465.3
2021-01-01	833783.3	970326.2	970274.7	836951.5
2021-02-01	759358.2	844881.3	858123.0	771180.4
2021-03-01	715165.1	837863.3	850620.9	736375.9
2021-04-01	724125.8	753733.2	758652.2	740698.3
2021-05-01	787027.2	838567.7	837417.8	756160.4
2021-06-01	1051774.8	1045829.5	1048767.9	782749.2
2021-07-01	1199673.3	1220059.1	1260127.2	1308443.8
2021-08-01	1223328.0	1224309.1	1266243.4	1156741.0
Source: US Energy Information Adminstration
¹ Thousand Mcf