NNAR

Introduction

The simplest network contains no hidden layers and are equivalent to linear regression. The coefficients attached to the predictors are called weights. The forecasts are a result of a linear combination of the inputs.

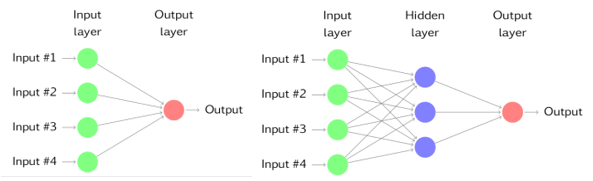
Once we add an intermediate layer with hidden neurons, the neural network becomes non-linear. This is known as a multi-layer feedforward network, where output of one node is the input of the next layer. The inputs are combined using a weighted linear combination.

The weights are random values to begin with, then are updated while training of the network. The aim of training is to find optimal values of these weights so that the overall error is minimized.

Neural Network AutoRegression

With time series, the lagged values of the series can be used as inputs to a neural network. We call such a network, Neural Network AutoRegression or NNAR Model.

It is denoted by NNAR(p,k) where ‘p’ is the number of lags (AR(p)) and ‘k’ is the number of hidden nodes in the network.

NNAR can model seasonal data as well. It is denoted by NNAR(p,P,k) where ‘P’ is the number of seasonal lags (SAR(P)).

In R, value of autoregressive and seasonal lags are automatically selected based on information criterion like AIC. For a seasonal time series, the default values are P = 1 and ‘p’ is chosen from the optimal model fitted to seasonally adjusted data. If ‘k’ is not specified, k = (p+P+1)/2.

Data Preparation

For training the model we use first 236 values and the remaining 12 values are used to test the prediction power of the model for our data.

#Load Data and Library
data = read.csv("data.csv")[,3]
date = read.csv("data.csv")[,1]
date = as.Date(date, format = "%d/%m/%Y")

library(forecast)

#Training Data
train = ts(data[1:236], start=c(2001, 1), freq=12)

Model Construction

set.seed(2018)
fit1 = nnetar(train)
print(fit1)

## Series: train 
## Model:  NNAR(3,1,2)[12] 
## Call:   nnetar(y = train)
## 
## Average of 20 networks, each of which is
## a 4-2-1 network with 13 weights
## options were - linear output units 
## 
## sigma^2 estimated as 3.441e+09

Here, the fitted model has 3 Autoregressive Lags and 1 Seasonal Lag. It has 2 nodes in the hidden layer. The [12] indicates Monthly seasonal frequency.

The estimated value of \(\hat{\sigma}^2 = 58660.04^2\).

Prediction

library(ggplot2)
fcast1 = forecast(fit1, PI = TRUE, h=12)
autoplot(fcast1)

It seems that the underlying trend and seasonality have been captured well by the model.
The PI = TRUE tells R to compute Confidence Intervals. (PI stands for Prediction Intervals)
The h=12 tells R to predict 12 steps ahead.
The shaded regions represent the 90% and 97.5% Confidence Intervals respectively.

Plot

Here, we have a plot of the Actual and Predicted values for the last 12 months till Aug, 2021.
The black represents Actual and Red the Prophet-predicted values.
The yellow band is the 90% Confidence Interval.
A few observed values lie outside the Confidence Interval Band. This is bad news because it means that the model could not predict them properly.
Overall, the network seems to perform poorly for our dataset.

RMSE-MAPE

library(Metrics)
round(c(rmse(tail(data, 12), fcast1$mean),
        mape(tail(data, 12), fcast1$mean)),5)

## [1] 103600.35006      0.11076

High RMSE and MAPE figures conform the above conclusions.

Output Table

U.S. Consumption of Electricity Generated by Natural Gas
Dates	Actual¹	Prediction¹
2020-09-01	1006071.1	1050016.1
2020-10-01	924056.2	961640.7
2020-11-01	737935.2	883412.8
2020-12-01	839912.6	907450.1
2021-01-01	833783.3	954538.1
2021-02-01	759358.2	931923.5
2021-03-01	715165.1	900179.7
2021-04-01	724125.8	823021.7
2021-05-01	787027.2	827470.3
2021-06-01	1051774.8	989863.4
2021-07-01	1199673.3	1253110.1
2021-08-01	1223328.0	1278392.4
Source: US Energy Information Adminstration
¹ Thousand Mcf